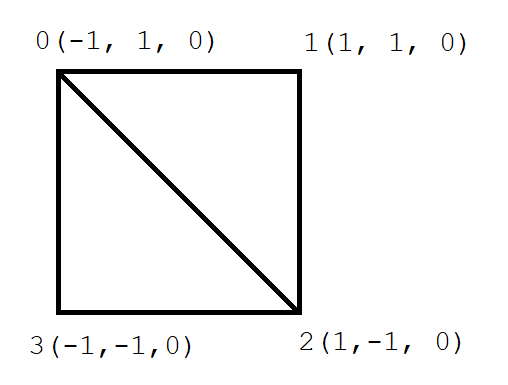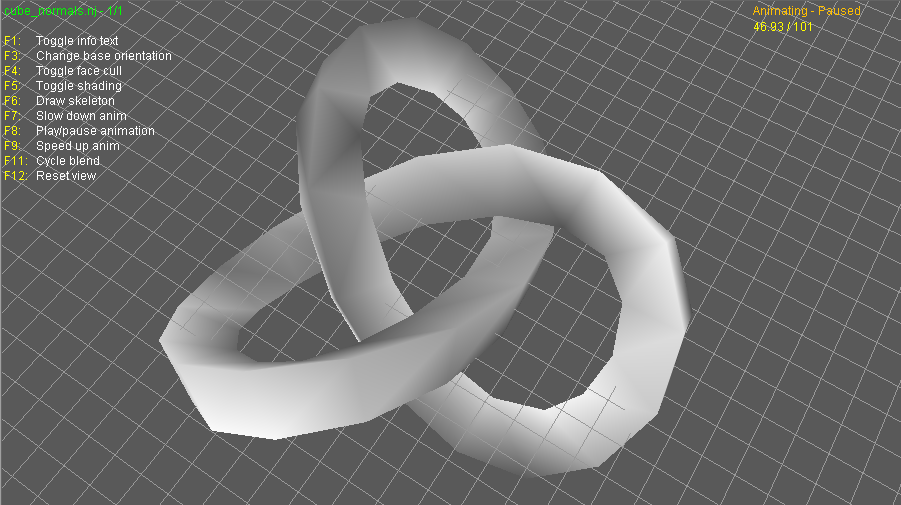Ninja ASCII (.NJA) format conversion from .OBJ [Theory]

[egg yolk]

For a while now it has been known that with the Dreamcast Development Kit (DDK), it is possible to export PSOBB model files known as Ninja Chunk Models (NJ) and ASCII versions of those models (NJA) from 3DS MAX 2.5/3.0, with the use of an old Windows virtual machine (VM).

To describe NJA, it is a readable version of an NJ file, and the documentation in the DDK explains most of what is going on in NJA files. The reason NJA has recently become important, is because there is another tool in the DDK (njaconv.exe) that can convert NJA files to NJ without the need of a VM or 3DS MAX, since njaconv.exe still works in Windows 10 as a command line tool. njaconv.exe has a lot of similarities to the 3DS MAX exporter in terms of options and capabilities, the only issue here is that it's still required to use a VM to produce an NJA file, which is needed to make use of njaconv.exe.

With the mentioned resources I decided to start reverse engineering NJA to hopefully remove the need of using a VM to make custom models. The end goal is to have a tool that converts an OBJ (possibly a different format) to NJA, and then using njaconv.exe to convert NJA to NJ. I am using this forum to post my findings similar to a Kion or blog thread, since I think it is a good location for those interested to learn about it and possibly help out. For this first post, I have carried out several tests to help prove that it should be possible, but it is a large task, and this is only the beginning of my attempt to figure out NJA files, so I am by no means saying this will be finished anytime soon. I am also quite amateur when it comes to floating point conversions, so please let me know if I am doing something wrong.

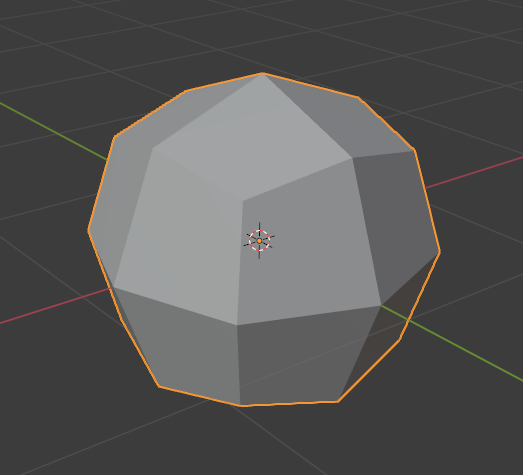
This is the model I have been using for the first few tests, the reason for this model, is that it gives a varied amount of different XYZ coordinates based on it's vertices. I have exported this model as an OBJ file, and again as an NJA file through VM. Thanks to DOOMGUY for helping me out with a new VM!

​

Below are my findings:

Spoiler: Test 1: njaconv.exe format testing

The first test is to see which header types can be created with njaconv.exe, to do this I created two versions of the above model with and without a texture as NJA files.

Next I converted those NJA files with njaconv.exe into NJ files, as expected, an NJ with the header NJTL was created from the NJA with a texture, and an NJ with the header NJCM was created from the NJA without a texture.

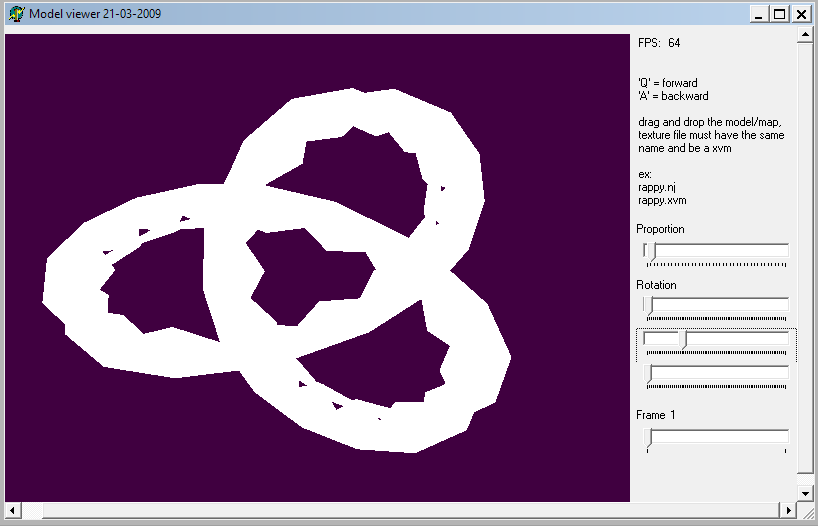
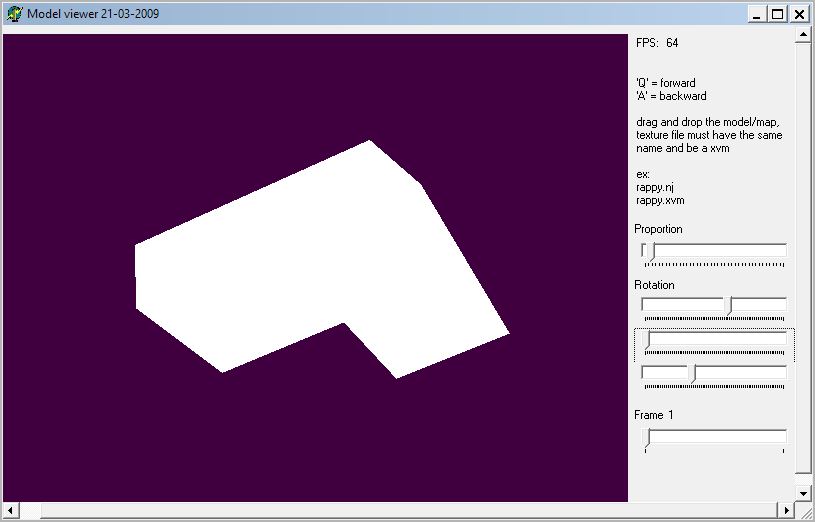
I also tested that these models ran in Model View, which they did, this basically means the models would be viable for replacements in PSOBB and that njaconv.exe is a possible solution to avoiding VM usage.

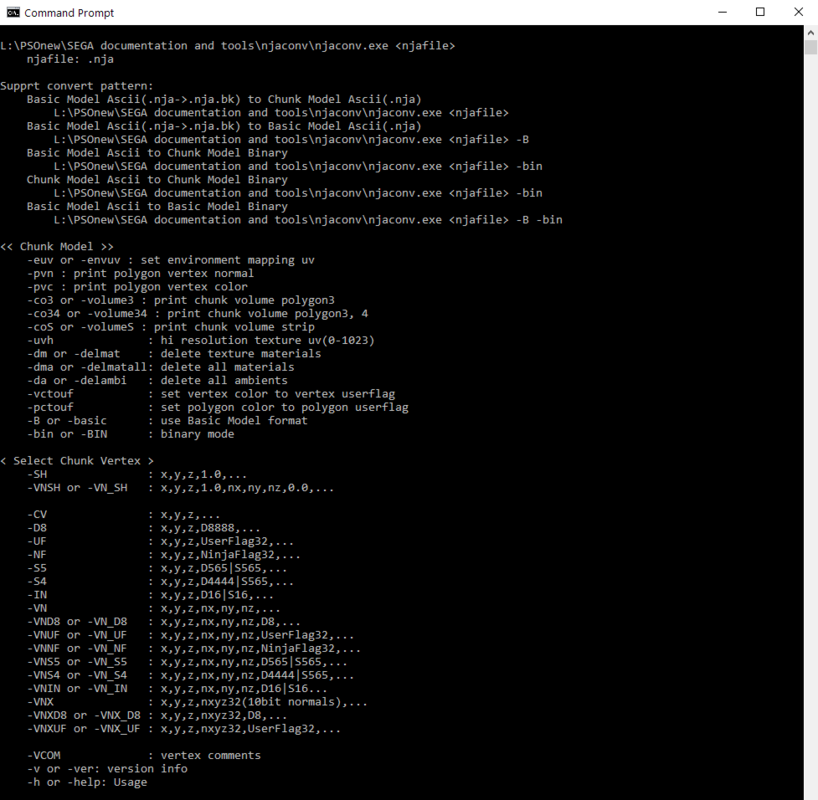
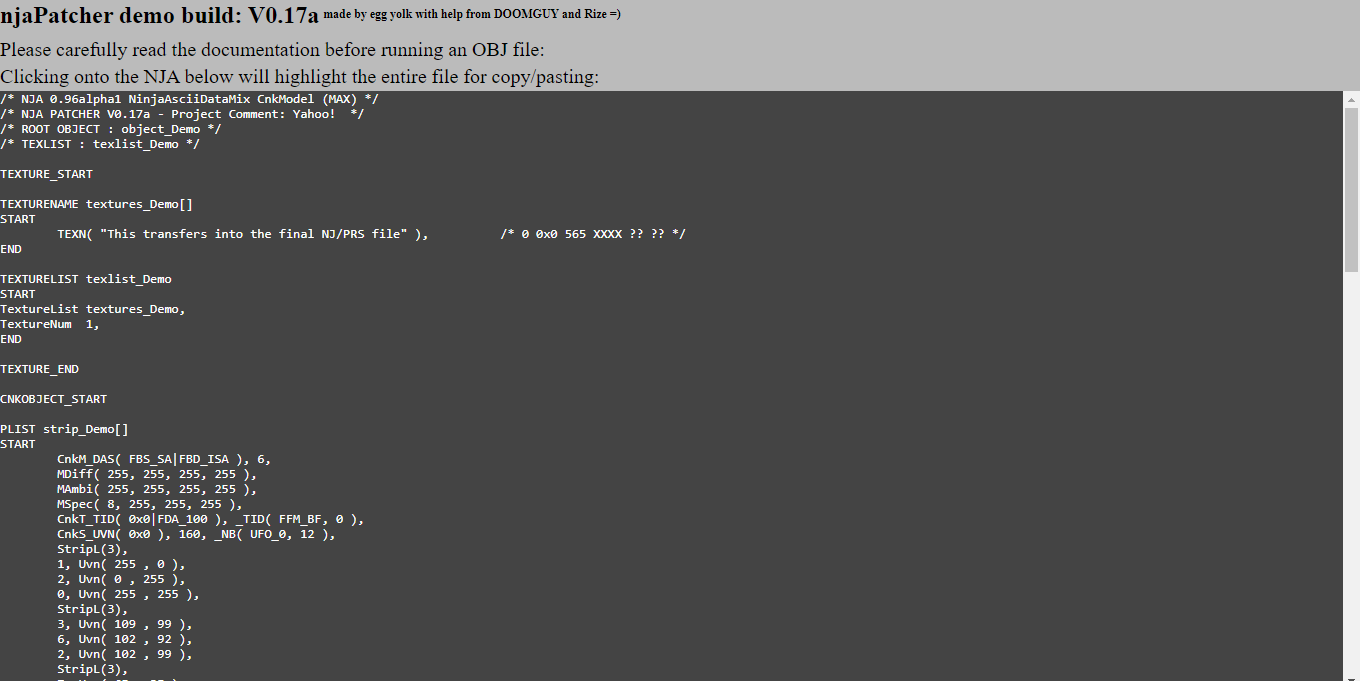
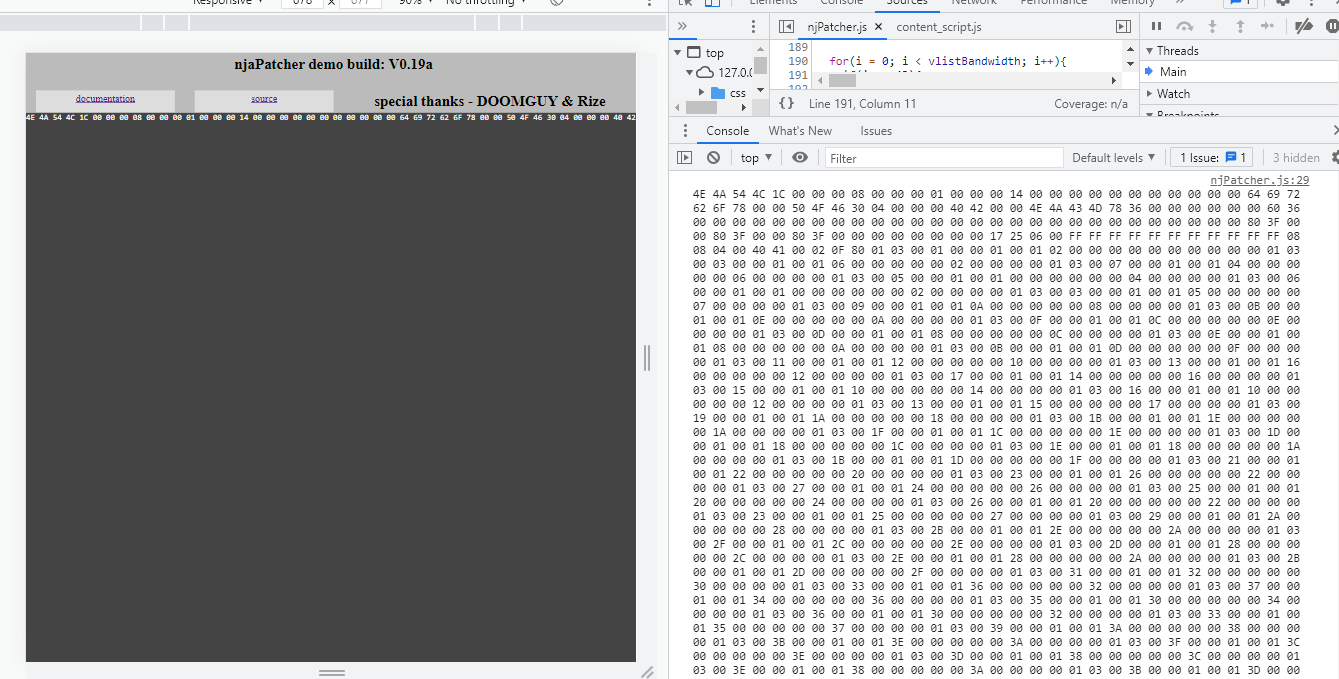
This is what njaconv.exe looks like for context, I used the -bin option:

​

Spoiler: Test 2: Vertex matching between NJA and OBJ

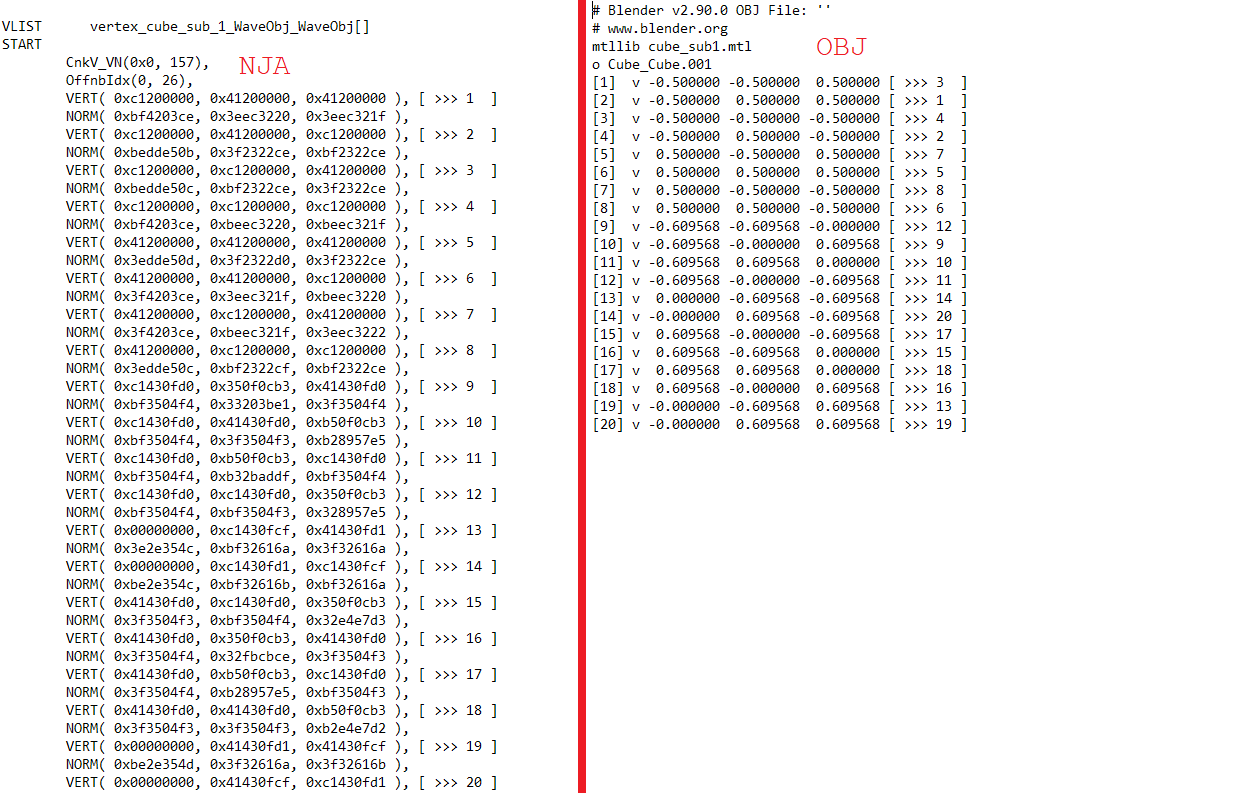
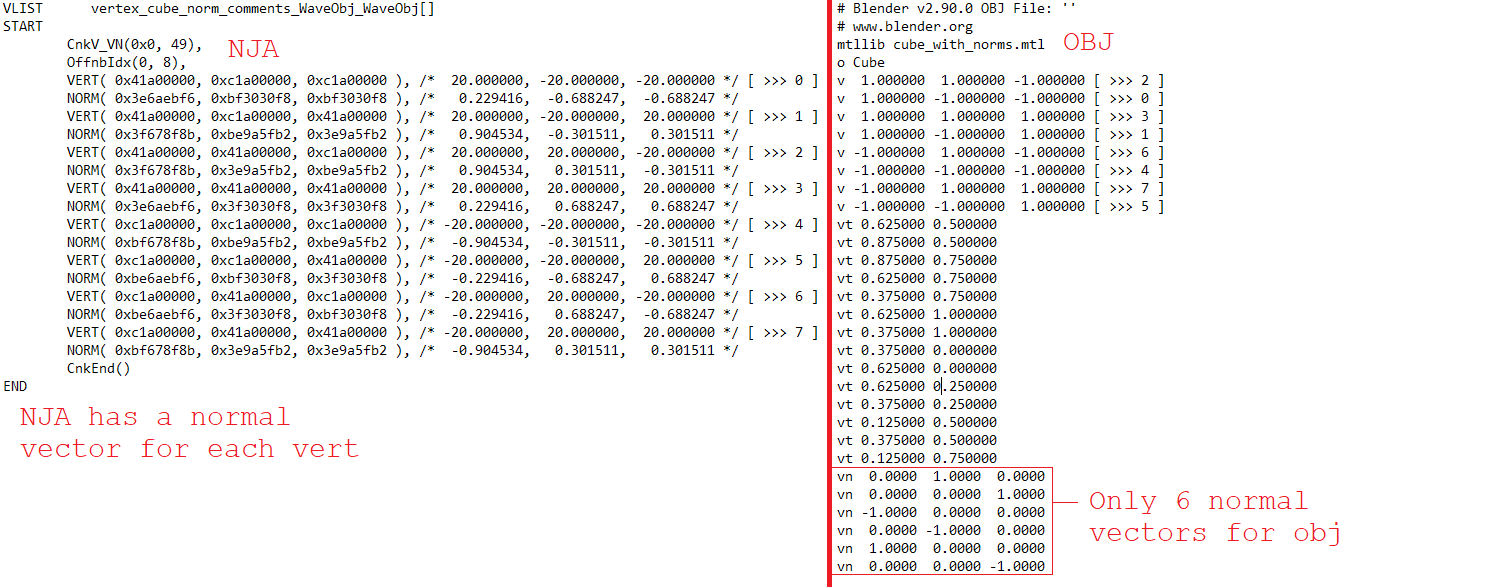
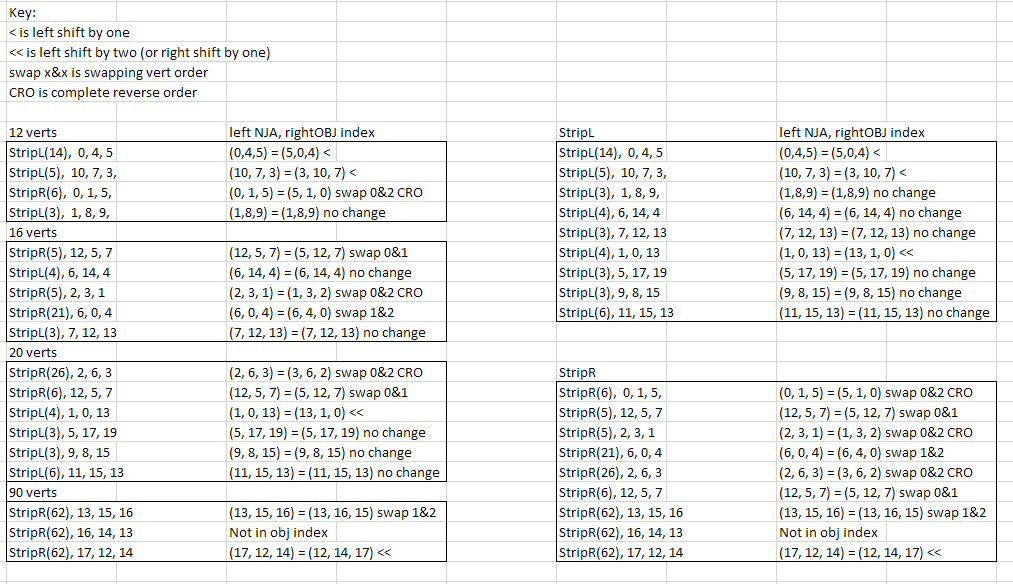
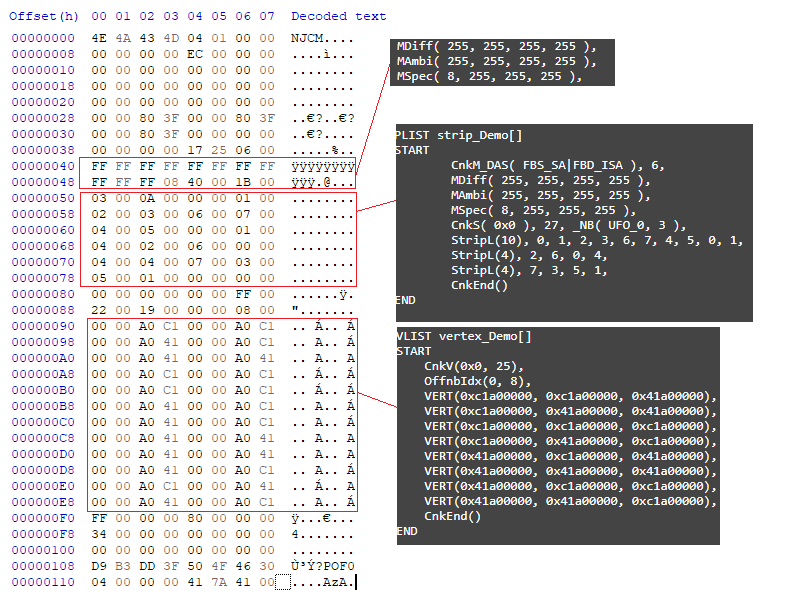
With the help of a friend (Rize), we were able to figure out that NJA lists it's vertex values as floating points, but they are displayed as hexadecimal values in the NJA file. This took some trial and error to figure out, but I have mapped out the original shape shown in the opening, as a cross comparison between it's NJA and OBJ file. The parts in the below screenshot surrounded with "[ ]" were added in by myself, to show which vertices from NJA match those in OBJ.

The hope was that there would be some kind of order in the OBJ file to make this part a bit easier, but it doesn't seem to be the case. Either way, we figured out the formula for preparing the OBJ values to floating point. NJA values are simply 20 times the amount of OBJ values, and are converted to hexadecimal, I'm personally unsure if we are using the wrong type of floating point converter here, but it works anyway. This is the converter we used: https://www.h-schmidt.net/FloatConverter/IEEE754.html

​

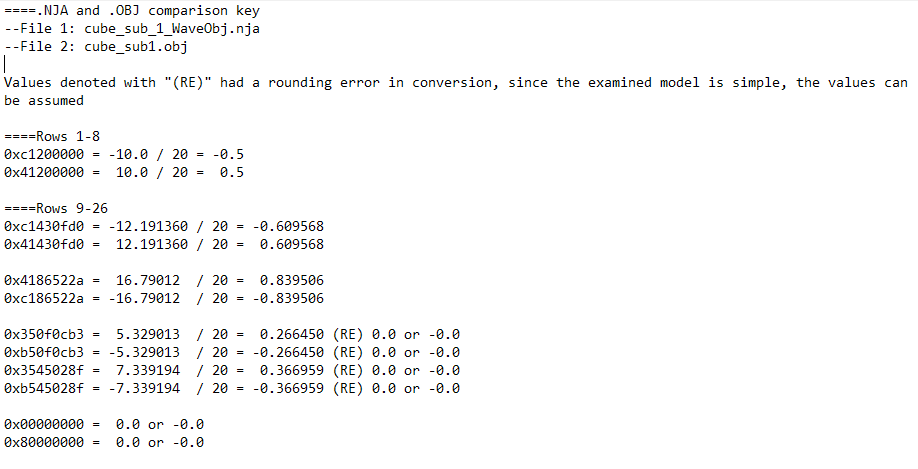
While doing this comparison I also made a key, to show how the NJA values match the OBJ values. There were some rounding errors in the process, mostly where values were negative zero, but also sometimes when they were just zero, so the next test is to replace all negative zero values with 0x00000000 and to see if the file still converts using njaconv.exe.

​

Spoiler: Test 3: Change rounding error values to 0x00000000

Using the key from before, I replaced all vert entries with rounding errors to just contain 0x00000000. Following this I ran this modified file through njaconv.exe, and sure enough the file converted correctly to NJ.

I also tested it in Model View to see if any of the verts were messed up, but it worked fine! This means there will have to be some detection for rounding errors in the tool, that just converts them to 0x00000000.

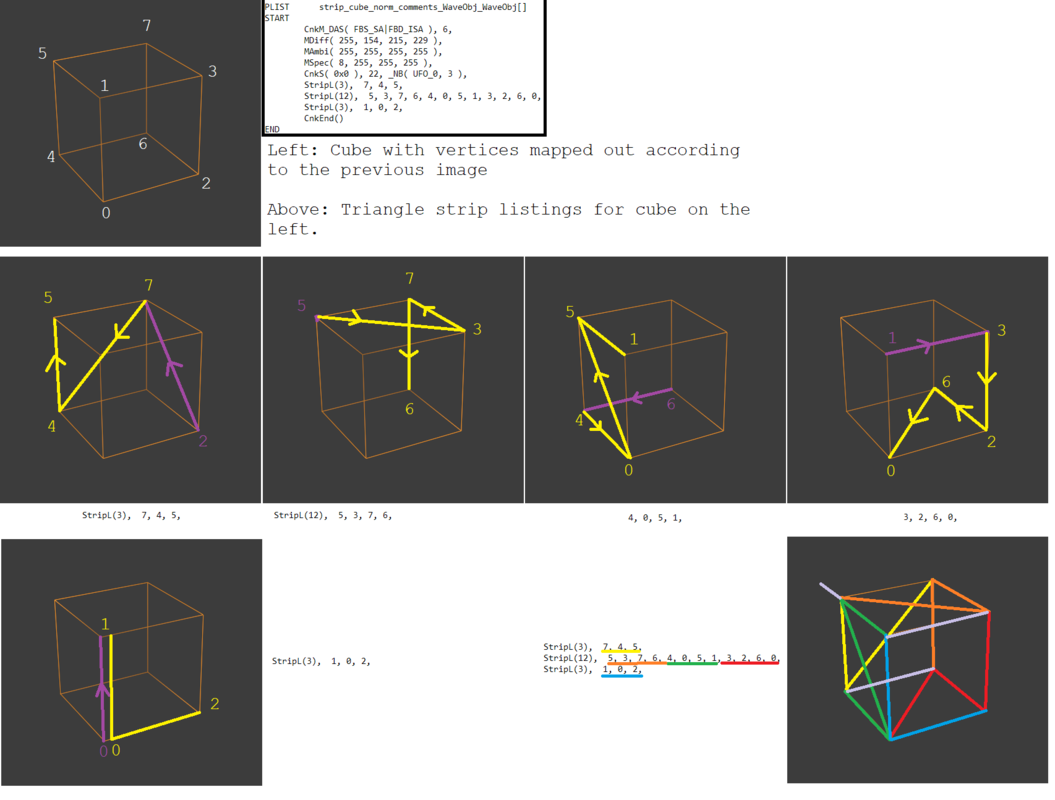
With those tests done, the next step is to take a look at normal values, which at the moment I assume are also just x20 of the OBJ counterparts. I will link the full NJA file below as embedded code if anyone wants to see it, the hard parts will likely be triangle strips and texture mapping but for now I am only working on an NJA without texture mapping. Everything else seems pretty trivial.

Spoiler: Embedded NJA

/* NJA 2.11.00 Ninja2AsciiDataMix CnkModel (MAX) */

/* ROOT OBJECT : object_cube_sub_1_WaveObj_WaveObj n(1) d(1) v(26) */


CNKOBJECT_START

PLIST      strip_cube_sub_1_WaveObj_WaveObj[]
START
    CnkM_DAS( FBS_SA|FBD_ISA ), 6,
    MDiff( 255, 153, 228, 184 ),
    MAmbi( 255, 255, 255, 255 ),
    MSpec( 8, 255, 255, 255 ),
    CnkS( 0x0 ), 67, _NB( UFO_0, 6 ),
    StripR(18),  3, 20, 11, 8, 2, 24, 12, 15, 6, 22,
                   14, 16, 7, 25, 13, 10, 3, 20,
    StripR(6),  11, 2, 21, 12, 14, 6,
    StripR(6),  14, 7, 21, 13, 11, 3,
    StripR(18),  22, 5, 16, 19, 25, 1, 10, 9, 20, 0,
                   8, 18, 24, 4, 15, 17, 22, 5,
    StripR(6),  17, 4, 23, 18, 9, 0,
    StripR(6),  9, 1, 23, 19, 17, 5,
    CnkEnd()
END

VLIST      vertex_cube_sub_1_WaveObj_WaveObj[]
START
    CnkV_VN(0x0, 157),
    OffnbIdx(0, 26),
    VERT( 0xc1200000, 0x41200000, 0x41200000 ),
    NORM( 0xbf4203ce, 0x3eec3220, 0x3eec321f ),
    VERT( 0xc1200000, 0x41200000, 0xc1200000 ),
    NORM( 0xbedde50b, 0x3f2322ce, 0xbf2322ce ),
    VERT( 0xc1200000, 0xc1200000, 0x41200000 ),
    NORM( 0xbedde50c, 0xbf2322ce, 0x3f2322ce ),
    VERT( 0xc1200000, 0xc1200000, 0xc1200000 ),
    NORM( 0xbf4203ce, 0xbeec3220, 0xbeec321f ),
    VERT( 0x41200000, 0x41200000, 0x41200000 ),
    NORM( 0x3edde50d, 0x3f2322d0, 0x3f2322ce ),
    VERT( 0x41200000, 0x41200000, 0xc1200000 ),
    NORM( 0x3f4203ce, 0x3eec321f, 0xbeec3220 ),
    VERT( 0x41200000, 0xc1200000, 0x41200000 ),
    NORM( 0x3f4203ce, 0xbeec321f, 0x3eec3222 ),
    VERT( 0x41200000, 0xc1200000, 0xc1200000 ),
    NORM( 0x3edde50c, 0xbf2322cf, 0xbf2322ce ),
    VERT( 0xc1430fd0, 0x00000000, 0x41430fd0 ),
    NORM( 0xbf3504f4, 0x33203be1, 0x3f3504f4 ),
    VERT( 0xc1430fd0, 0x41430fd0, 0xb50f0cb3 ),
    NORM( 0xbf3504f4, 0x3f3504f3, 0xb28957e5 ),
    VERT( 0xc1430fd0, 0xb50f0cb3, 0xc1430fd0 ),
    NORM( 0xbf3504f4, 0xb32baddf, 0xbf3504f4 ),
    VERT( 0xc1430fd0, 0xc1430fd0, 0x00000000 ),
    NORM( 0xbf3504f4, 0xbf3504f3, 0x328957e5 ),
    VERT( 0x00000000, 0xc1430fcf, 0x41430fd1 ),
    NORM( 0x3e2e354c, 0xbf32616a, 0x3f32616a ),
    VERT( 0x00000000, 0xc1430fd1, 0xc1430fcf ),
    NORM( 0xbe2e354c, 0xbf32616b, 0xbf32616a ),
    VERT( 0x41430fd0, 0xc1430fd0, 0x00000000 ),
    NORM( 0x3f3504f3, 0xbf3504f4, 0x32e4e7d3 ),
    VERT( 0x41430fd0, 0x00000000, 0x41430fd0 ),
    NORM( 0x3f3504f4, 0x32fbcbce, 0x3f3504f3 ),
    VERT( 0x41430fd0, 0x00000000, 0xc1430fd0 ),
    NORM( 0x3f3504f4, 0xb28957e5, 0xbf3504f3 ),
    VERT( 0x41430fd0, 0x41430fd0, 0x00000000 ),
    NORM( 0x3f3504f3, 0x3f3504f3, 0xb2e4e7d2 ),
    VERT( 0x00000000, 0x41430fd1, 0x41430fcf ),
    NORM( 0xbe2e354d, 0x3f32616a, 0x3f32616b ),
    VERT( 0x00000000, 0x41430fcf, 0xc1430fd1 ),
    NORM( 0x3e2e354d, 0x3f32616b, 0xbf32616a ),
    VERT( 0xc186522a, 0x00000000, 0x00000000 ),
    NORM( 0xbf800000, 0x00000000, 0x00000000 ),
    VERT( 0x00000000, 0xc186522a, 0x00000000 ),
    NORM( 0x3316e3e0, 0xbf800000, 0x335ace42 ),
    VERT( 0x4186522a, 0x00000000, 0x80000000 ),
    NORM( 0x3f800000, 0x31af0b68, 0x31af0b68 ),
    VERT( 0x00000000, 0x4186522a, 0xb545028f ),
    NORM( 0x3284d79f, 0x3f800000, 0xb35ace42 ),
    VERT( 0x00000000, 0x00000000, 0x4186522a ),
    NORM( 0xb233442a, 0x3383488e, 0x3f800000 ),
    VERT( 0x00000000, 0x00000000, 0xc186522a ),
    NORM( 0xb2b09a79, 0xb344ecd5, 0xbf800000 ),
    CnkEnd()
END

CNKMODEL   model_cube_sub_1_WaveObj_WaveObj[]
START
VList      vertex_cube_sub_1_WaveObj_WaveObj,
PList      strip_cube_sub_1_WaveObj_WaveObj,
Center       0.000000F,  0.000000F,  0.000000F,
Radius      17.320509F,
END

CNKOBJECT  object_cube_sub_1_WaveObj_WaveObj[]
START
EvalFlags ( FEV_UT|FEV_UR|FEV_US|FEV_BR ),
CNKModel   model_cube_sub_1_WaveObj_WaveObj,
OPosition  (  0.000000F,  0.000000F,  0.000000F ),
OAngle     (  0.000000F,  0.000000F,  0.000000F ),
OScale     (  1.000000F,  1.000000F,  1.000000F ),
Child       NULL,
Sibling     NULL,
OQuatRe    ( 0.000000 ),
END

CNKOBJECT_END


DEFAULT_START

#ifndef DEFAULT_OBJECT_NAME
#define DEFAULT_OBJECT_NAME object_cube_sub_1_WaveObj_WaveObj
#endif

DEFAULT_END

​

 

[DOOMGUY]

Once again. Amazing work brother. If there's any lurkers interested in this line of investigation msg me for a Discord link.

 

[egg yolk]

I did some more study of the NJA format over the past day, looking at normals and triangle strips, this time looking at a model of a simple cube to the scale of 1.0.

First of all, the NJA format seems to calculate normals for each vertex vector, which is quite different to how OBJ works, since OBJ writes normal vectors only for each face. Through looking at the Ninja documentation in the DDK, I am assuming that the normals in NJA are based off edges rather than faces, this would make sense since there are as many normal vectors as there are vertex vectors, but I am still unsure how they are calculated for now. Something I will do for the next look at normals, is make a cube OBJ that is 20 times smaller, so then the VERT and NORM values should be more relevant, i.e. rather than a vector of (20.000000, -20.000000, -20.000000), it would be (1.000000, -1.000000, -1.000000).



Fortunately, I realized that when enabling comments in the exporter, it actually prints float values along side the VERT and NORM sections, which can be seen above. While frustrating since we just figured this out ourselves the other day, it will be useful to not have to hand convert hexadecimal to floating point, and it also confirms that we were on the right track.

I also had a look at triangle strips, I don't think my diagram is overly useful, but I think it is a step in the right direction. A few notes about it before taking a look. I mapped out the coordinates of the vertices using the NJA file above, then I sketched the links between each vertex vector regarding the triangle strip notation, which can be seen in the next image. What I learned from doing this, is the triangle strip notation doesn't occupy all edges of the cube, which is likely something I am missing, I think it is related to strip direction, which is denoted as StripL(X) or StripR(X), I don't fully understand this part yet, but I believe I can read more about it in the Ninja documentation. One thing I did learn is that the strips never crossed through the object in my test, which I think is a good sign and indicates how a triangle strip drawing algorithm might be written. Lastly, the lines seen as purple (and lilac in the final image) are intended to be the links between the last part of a strip section, and the first part of the next strip section. I think I will attempt this again soon.

 

[egg yolk]

Small update today. First off, I am going to put a list of artifacts at the bottom of this post to make the structuring a bit easier to follow, I will tag them as figures throughout the post.

I will announce that I have been writing a script in JavaScript for patching NJA files (named js-njaPatcher), it generates a new NJA file based on parameters from an OBJ file. So far it has IEEE-754 floating point conversion [Figure 1] for VERT values and can write unoptimized lists of triangles. The focus of the script for the time being is to create non textured objects that work with njaconv.exe, since there is a form of NJ (NJCM) that doesn't need normal values or texture coordinate values. The script is not currently in a usable state, so I won't share it here just yet, you can search for it on GitHub if you wish to take a look, but I don't recommend using it for anything right now.

EDIT: Not recommended to search for project, it's not up to date, since the core optimization is not ready yet.

The next release of the script is able to create very limited shapes [Figure 2], it can accurately produce shapes with 8 vertices for now, although I have only tested it with a cube drawing, this issue is confirmed to come from the triangle strips generation, and I believe that solving them will ultimately allow for generating any untextured model from Blender into NJA, and then into NJ (NJCM) without using virtual machine. These types of models "NJCM" are the same ones that cause the "phase shift" effect [Figure 3] when you replace a slicer model in PSOBB, but they are also used throughout PSOBB for static scenery objects like the Christmas trees near the bank for example.

So, about triangle strips, I can confirm that my previous attempt at solving them was half correct and I will explain why with some psuedo code.

Below is a definition of a cube as a set of data points or vertices, that are then indexed in a list.

VERT0 = (-1, -1,  1),
VERT1 = (-1,  1,  1),
VERT2 = (-1, -1, -1),
VERT3 = (-1,  1, -1),
VERT4 = ( 1, -1,  1),
VERT5 = ( 1,  1,  1),
VERT6 = ( 1, -1, -1),
VERT7 = ( 1,  1, -1),

cube_data_points = [VERT0, VERT1, VERT2, VERT3, VERT4, VERT5, VERT6, VERT7]

With these data points, triangle strips can be drawn. Below I will show how these verts can construct each triangle that makes up a cube.

//Instead of writing "cube_data_points[0], cube_data_points[1], etc.",
//I will refer to each index of "cube_data_points" as individual indices.

TriangleStrip0  = 0, 1, 2 //Left bottom half
TriangleStrip1  = 2, 1, 3 //Left top half
TriangleStrip2  = 3, 2, 6 //Back bottom half
TriangleStrip3  = 6, 3, 7 //Back top half
TriangleStrip4  = 6, 7, 4 //Right bottom half
TriangleStrip5  = 4, 5, 7 //Right top half
TriangleStrip6  = 5, 4, 0 //Front bottom half
TriangleStrip7  = 5, 0, 1 //Front top half
TriangleStrip8  = 5, 1, 3 //Roof bottom half
TriangleStrip9  = 5, 3, 7 //Roof top half
TriangleStrip10 = 0, 4, 2 //Floor bottom half
TriangleStrip11 = 0, 6, 4 //Floor top half

So far, what I have described is how I understood triangle strips using my initial approach in the previous post. The problem with this approach is that it's extremely unoptimized, you can see in the generated NJA file [Figure 2] that this is how my script currently generates triangle strips, and while it will work for objects with low amounts of vertices, it quickly runs out of memory when converting more complex shapes. While complex shapes can still be converted, they appear as corrupted models instead, where sometimes just part of the model is drawn in ModelView [Figure 4].

To fix this, an algorithm needs to be written that sorts the vertex indices in a way that data can be reused. Take a look at this strip generated from SEGAs exporter of the same cube described above.

StripL(10),  7, 4, 6, 0, 2, 1, 3, 5, 7, 4,

This strip actually draws the entire outside of the cube in way less instructions, the way it works is, rather than defining each triangle verbatim, it uses the same data points for multiple triangles, for example, (7, 4, 6), and (4, 6, 0) are different triangles, but use the same data. This is the actual reason triangle strips are used in general, because of this optimization; by reusing data like this a lot of memory is saved.

My next arc of this project will involve using the above strip from SEGAs exporter as a reference to ordering my own triangles with a new algorithm. It should be a recursive algorithm that reorders triangles from OBJ. I do indeed have all the data required to write this algorithm now, so I will attempt to do it in the coming weeks.

There is a lot of other stuff I have discovered about NJA, but I will leave it for the documentation of the script, I do have an understanding of nearly every aspect of NJA now, with the exception of how normals and texture coordinates are generated, there are more tests to do with those however, and it will be a while until I look at them again.

That is my update for now! Thanks for reading. =)

Figure 1: IEEE-754 floating point conversion in JavaScript by Nina Scholz
https://stackoverflow.com/questions...it-hex-string-in-javascript/47187116#47187116

Figure 2: Generated NJA file

Spoiler

/* NJA 2.11.00 Ninja2AsciiDataMix CnkModel (MAX) */
/* NJA PATCHER V0.1 Project Comment: cube because only simple shapes work  */
/* ROOT OBJECT object_small_cube */

CNKOBJECT_START

PLIST strip_small_cube[]
START
    CnkM_DAS( FBS_SA|FBD_ISA ), 6,
    MDiff( 255, 255, 255, 255 ),
    MAmbi( 255, 255, 255, 255 ),
    MSpec( 8, 255, 255, 255 ),
    CnkS( 0x0 ), 144, _NB( UFO_0, 20 ),
    StripL(3), 1,2,0,
    StripL(3), 3,6,2,
    StripL(3), 7,4,6,
    StripL(3), 5,0,4,
    StripL(3), 6,0,2,
    StripL(3), 7,0,5,
    StripL(3), 0,0,0,
    StripL(3), 1,0,3,
    StripL(3), 5,8,1,
    StripL(3), 3,0,7,
    StripL(3), 1,3,2,
    StripL(3), 3,7,6,
    StripL(3), 7,5,4,
    StripL(3), 5,1,0,
    StripL(3), 6,4,0,
    StripL(3), 7,0,0,
    StripL(3), 0,8,0,
    StripL(3), 1,8,0,
    StripL(3), 5,0,8,
    StripL(3), 3,0,0,
   
    CnkEnd()
END

VLIST vertex_small_cube[]
START
    CnkV(0x0, 37),
    OffnbIdx(0, 12),
   
    VERT(0xc1a00000, 0xc1a00000, 0x41a00000),
    VERT(0xc1a00000, 0x41a00000, 0x41a00000),
    VERT(0xc1a00000, 0xc1a00000, 0xc1a00000),
    VERT(0xc1a00000, 0x41a00000, 0xc1a00000),
    VERT(0x41a00000, 0xc1a00000, 0x41a00000),
    VERT(0x41a00000, 0x41a00000, 0x41a00000),
    VERT(0x41a00000, 0xc1a00000, 0xc1a00000),
    VERT(0x41a00000, 0x41a00000, 0xc1a00000),
    VERT(0xc1a00000, 0x42700000, 0x41a00000),
    VERT(0xc1a00000, 0x42700000, 0xc1a00000),
    VERT(0x41a00000, 0x42700000, 0xc1a00000),
    VERT(0x41a00000, 0x42700000, 0x41a00000),
    CnkEnd()
END

CNKMODEL model_small_cube[]
START
VList      vertex_small_cube,
PList      strip_small_cube,
Center       0.000000F,  0.000000F,  0.000000F,
Radius       1.732051F,
END

CNKOBJECT object_small_cube[]
START
EvalFlags ( FEV_UT|FEV_UR|FEV_US|FEV_BR ),
CNKModel   model_small_cube,
OPosition  (  0.000000F,  0.000000F,  0.000000F ),
OAngle     (  0.000000F,  0.000000F,  0.000000F ),
OScale     (  1.000000F,  1.000000F,  1.000000F ),
Child       NULL,
Sibling     NULL,
OQuatRe    ( 0.000000 ),
END

CNKOBJECT_END

DEFAULT_START

#ifndef DEFAULT_OBJECT_NAME
#define DEFAULT_OBJECT_NAME object_small_cube
#endif

DEFAULT_END

Figure 3: "Phase shifting" with NJCM models

Figure 4: Corrupted model in ModelView, vs. actual model in Blender (12 vertices)

Spoiler

 

[egg yolk]

Some updates have been made for js-njaPatcher today, that I actually think it's worth sharing now (but not worth using for mods). You can find the repo below. If you wish to mess with it, you'll need to run it on a live server for the time being. If you just want to look and see how it works, I have tried to comment the important parts of the code. I might look at integrating it into a desktop application later, but this works well for doing tests at the moment.

EDIT: The repo is removed for now, planning to change license to some GNU so that any modifications have to be open sourced.

The main changes are that it can actually draw complex shapes from OBJ now, since the triangle strip generation problem is half solved. The current script for generating triangle strips does have some big issues though,

Issue 1: The script doesn't yet know how to determine the strip winding order, e.g., StripL(X) or StripR(X). What this means is that there are some serious culling issues, where many of the triangles are facing the wrong way in the final output.

Issue 2: The script doesn't optimize very well for more complex shapes, and creates far more strips than it should for complex shapes. I have a feeling this can be fixed though, but I may need to break down a more complex strip structure as exported from the 3DS MAX exporter.

I am not really sure I can explain the triangle strips optimization algorithm in text right now, since I may alter it later, I will at least show some working models generated from njaPatcher below, culling issues can be seen on complex shapes, but they are also present on basic shapes, ModelView just doesn't show it.

Spoiler: Generated shapes

A torus knot with major backface culling issues present:



A simple L shaped box, culling not present, but definitely not correct, can see that the shape is still drawn accurately though.

^^b​

 

[egg yolk]

I have started to do more research into SEGA's winding order algorithm for triangle strips, and have found some interesting results and will explain them below.

Just to note, (x, x, x) is equivalent to triangle(vert, vert, vert).

Firstly, I will describe how winding order (the order of verts in a triangle when read by a machine) changes the outcome of a polygonal model.

With the below image it can be imagined that (0, 1, 2) is one triangle and that (2, 0, 3) is the next triangle, so the entire quad could be (3, 0, 2, 1) as drawn in one direction, or (1, 2, 0, 3) in the opposite direction, the direction of faces in triangle strips is an arbitrary feature which changes between renderers, for instance, in one renderer (3, 0, 2, 1) might be drawn facing away from X (imagine X as a player character), whereas in a different renderer it might be drawn facing towards X.

​

The reason this is important is because .NJA has specification for the direction of a triangle strip. Denoted as StripL() and StripR() in an NJA file. Knowing this, I decided to try and figure out what makes a strip become StripL() and what makes a strip become StripR() by using exported NJA files as a reference.

Before describing this, it should be known that the OBJ file to be converted provides a look up table for all triangles that create the shape, the main way I have gathered these findings is through comparing SEGA exported NJA files with the associated OBJ's triangle look up table.

My findings are that, if the strip starts with a value (0,4,5) in a SEGA NJA file, and that value is in the same order as the value provided from an OBJ file then the strip will be denoted with StripL(), but that's not the only caveat to it.

The value (0,4,5) comes from the OBJ index (5,0,4), but they are not the same order, so how is it still StripL()? Well, StripL() can also start with the OBJ index when it has been shifted left by 1 or 2 and that doesn't change the winding order of that vertex vector, e.g,

0,4,5 = 4,5,0 = 5,0,4
​

How can I be sure about this? Well, winding order is pretty well documented like this, it is a heuristic used for many triangle strip algorithms it seems, but I won't know for sure until it is coded. To further test this idea, I have created the below reference for different NJA files and their associated OBJ files which shows the triangles in which each strip starts with, it should be noted that these strips do not create a full shape, since only the first triangle per strip is important for this particular test.



As can be seen, all StripL() values from the SEGA exported NJA files have either no change, or are shifted left by 1 or 2, it can also be seen that most StripR() values are either in reverse order, or have their first and last index swapped. This can also be easily proven by drawing a simple quad with the different actions.

There is one problem in this reference within the StripR() section for the object with 90 verts. What I found with this shape was that it contained a triangle which was not part of the OBJ index of triangles, not only that but it also left shifts at the start of a right strip. My theory here is that for some optimization, SEGAs conversion made an extra vert that is overlapping with another one. So perhaps if this optimization occurs, then the next strip is a StripR() except with the conditions of a StripL() (or vice versa), this will require more testing, but the reason I think this is because I was reading about something similar here (Connecting Strips section): http://www.codercorner.com/Strips.htm

The next question is, how can you determine which operation to perform on a starting triangle? Personally I believe SEGA's algorithm probably checks ahead to see which action creates the longest triangle strip (or set of strips, not sure yet), this is what I will try in code next, there could also be some kind of frequency check with the amount of shared verts per triangle, but I only started looking at that briefly and so far it is inconclusive.

 

[egg yolk]

Okay, so I actually implemented the findings from the previous post into my script and... It works... The triangle strips are still not completely optimized, but there are no culling issues anymore, meaning all of the triangles to be drawn are winded in the correct direction, this means that my script can now accurately convert OBJ models to NJA and then to NJ (NJCM) with njaconv.exe. I will show some comparisons between my scripts generated NJA files and 3DS MAX exported NJA files below, specifically triangle strip comparisons.

For the below comparisons, the left NJA is generated with njaPatcher, and the right NJA is made from the SEGA 3DS MAX exporter.

The first comparison is a cube model with 8 verts, the conversion is quite accurate here, the main difference is that SEGA's exporter probably checks for the best starting triangle, whereas my script just goes with the first available triangle, perhaps an optimization to implement later. The strip amount and length are identical, the only difference is the winding order, which in the left model, flips one of the roof or floor faces of the cube.

​

The second comparison is a torus knot with 90 verts (ignore the name after "PLIST"), from this image, it can be seen how different the two algorithms really are, despite producing the same shapes in the end, although it is clear that SEGA's exporter is far more optimized for higher vert counts. Something I am unsure about for now is how expensive it is in a game like PSOBB to run a model with as many triangle strips as my NJA models have, at the same time, I'm unsure if njaconv.exe fixes that when converting the model to NJ. Either way both torus knots as NJ format are the same file size, my NJA file is actually smaller than SEGA's too, not sure how.



With those comparisons I will show some new models that have been generated from njaPatcher and converted to NJ with njaconv.exe, this time I will show them in noesis, to show that no culling is present.

Torus knot (90 verts) from njaPatcher.


Collection of objects (95 verts) from njaPatcher
​

One last thing I will mention is that njaPatcher actually gets very slow when producing models of 200~+ verts, since the code is also quite unoptimized at the moment. In it's current state, if it had texture support, it would still be faster to convert a model in VM. The reason for the slowdown is probably the new look ahead that I have implemented today, where it essentially restarts per strip after checking for the best possible outcome, I do think that this slow down can be fixed through reducing the amount of generated strips in higher models though. For reference, a 90 vert model takes about 1 second to convert, but something with around 400 verts can take over 10 minutes. Hmm it could also be a memory leak, will have to check that another time.

Anyway, I am very happy with this progress! Thanks for reading~

​

 

[egg yolk]

Today I did get vertex normals to patch into an NJA file. Normals were not that complicated to implement in the end, since it's not necessary to mimic how the 3DS max exporter generates them, generally the normals provided from an OBJ file work just fine, so it was just a case of stripping the normal data from an OBJ and converting it to a format that njaconv.exe can read, which was the same as loading vertex entries, i.e., floating point conversion, which I am already using in the program, there is more about that in the first couple of posts here.

To show what normals are, it's basically values that describe the shading model of an object, you can see the difference between this model with normals below, and the ones in my previous post.

​

I didn't realize earlier, but if you load a model into PSOBB that doesn't have normals, it causes some bizarre effects to occur, where the model is confused about what it's supposed to represent and tries to morph into nearby objects, I'm not really sure why that occurs, I will probably post a video of it in time. On the other hand, if you load a model into PSOBB that does have normals, it functions like normal, and the full contents of the model can be seen, see images below.

​

Being able to load models like this allows me to test the limits of my script in terms of how viable the models are for running in PSOBB, e.g., does having less triangle strip optimization cause crashes? So far it seems fine, although I have only tested with a 90 vert model, and my previous mods from the exporter run with around 800-900 verts.

Something else is that I have further optimized my code, meaning that triangle strips for OBJ with 200-400 verts is pretty fast now, yet it still takes around 7 minutes to make one with 800+ verts, I still think I can optimize it further though, it's quite hard to optimize recursive code, but there should be something I'm missing, and even still, it should be possible to make the process iterative instead. In theory triangle strips should generate in linear time, but I had to add some extra stuff to meet the NJA specification.

Anyway, with normals and triangle strips implemented, the only other feature I would like to implement is textures, hopefully it is not that bad. I will probably make another post when I have tested higher vert models, and then again if I can implement textures.

 

[egg yolk]

Textures are not fully implemented at the moment, but I did create an NJA file with texture support today. This is quite valuable since, textures support generally makes objects in PSO behave more stable, for instance, flickering visual effects occur when using an NJ without textures.

I will probably try to patch a blank animation to the file since, it's almost a requirement at this point to get an item model to display, it could be visible flags relating to an animation function if I had to guess, not sure if SEGA would optimize the game to have animations playing while an object is not displaying.

I still need to remap the texture coords, but I have the data for it, so will try that next. I will post a better image when I have texture coords working but the model conversion to NJA also takes care of texture alpha (transparent texture) fortunately.

​

 

[egg yolk]

Texture mapping is now implemented, in order to get texture mapping to work I had to alter some of the triangle strip program, since NJA uses OBJ texture index as a base for triangle strips when it has a texture list (NJTL), previously (without textures) it used OBJ vertex index instead (NJCM). Hoping to support both of these modes, so that the script can generate different versions of NJA.

I haven't tested more abstract models with the new texture implementation yet, but that is what I will try next. Texture mapping at least works for the models I have converted so far (box and torus). Another issue with the script is that I'm not sure how the texture orientation is transferred just yet, it appears as if the texture coords are set to be upside down, this can be seen in the image from blender at the bottom of this post. Currently the script only supports a single texture, but I haven't looked at adding multiple textures yet and it's probably a feature I will sleep on for a while.

Upon implementing textures I have noticed some issues with the normal mapping, although it just means I have to apply different processing to normal coordinates, it shouldn't be too difficult to do with the current data structures in the script. You can see the incorrect normal coords in the below image, since the model isn't shaded according to the lighting.

​

 

[egg yolk]

Normals and textures should be fully supported now, they seem to be working fine in my recent tests. I made a reference NJ which shows where XYZ (red, green, blue) are facing, to ensure that the textures were mapped correctly, some oddities about this; through loading larger models I've noticed particles appear behind the weapon layer, and a cube like this shows the orientation of your weapon quite well for referring to it in Blender.

​

Another texture experiment I did was checking the OBJ export types that njaPatcher can currently use. As of now, it's required to triangulate the mesh in blender, and to use the shade smooth option on the model before it's exported from blender. It's probably possible to add support for quads in the future, and to maybe implement generative normals, so that even when a shade flat OBJ is exported from blender, the program would create it's own normals for smooth shading. Here is a more precisely mapped model with more verts to show texture mapping and normals working.

​

I can also say that the script is running a lot faster now, a 400 vert model can be processed in a around a second, due to how UVs work. Generally NJTL format has a lot more individual strips than NJCM has (making it easier to order). Technically it was unnecessary to write optimization scripts for triangle strips, but at least it is optimizing the NJA model in someway. There does seem to be a 'bandwidth' value in NJA that should be altered when there are more triangle strips and texture coords (higher 'bandwidth' requirement for more strips/coords), currently the script just makes this overshoot by a small amount, since I'm unsure exactly how it's calculated.

 

[egg yolk]

Should release njaPatcher as a demo build this weekend, since I plan to make njaPatcher into a lib with optional GUI (HTML/CSS, maybe node bundle). The demo build will include a HTML interface solely for copy and pasting, there is no drag and drop feature yet, so it requires that you have a code editor with live server installed (I use Atom, but Visual Studio Code might be the better choice). About the interface for the demo build, the core functionality is still stored in the header of the main script, so the systems aren't refactored yet.

​

I still need to write up some documentation for it, so I will do that next. In this state of the program, OBJ can transfer to NJA under a specific set of rules,

I use blender and paint.net so other editor options may vary.

1) Export as triangulated mesh (do this on export) (doesn't read quads yet)
2) Make sure shade smooth normals are enabled in the viewport editor (no flat shade detection) (will draw wrong normals if flat shade export)
3) Use a texture that is 256/256 (hard limit for now)
4) Export as single .OBJ and single texture .PNG -> .DDS
5) Don't write materials to OBJ, just need the correct UV coords to be applied to the object
6) Not recommended to set UV coords outside of the image

Those are all the requirements for creating an OBJ.

This creates a print of an NJA file (3D Model preference list), it's not the entire process of adding a model to PSOBB, but there are a bunch of tools required to compress the model after running the OBJ through njaPatcher, and then more tools to add the model into the PSOBB archive folders.

But, it is a 100% chance access to model transfer (specific items) in Windows 10/Chrome, and is usually just a case of remembering the pattern of programs to figure out your problem, there is no VM involved. The program determines whether the OBJ makes a different version of NJA also, such as, whether it is textured, or if it has a normal list. This was a feature in the original exporter also.

 

[egg yolk]

njaPatcher is now available as a demo version x) - https://github.com/je-mappelle-egg-yolk/njaPatcher

Currently the tool can directly transfer OBJ to NJA, but it is done through a code editor. I will not share this too widely as it's not a GUI application and might not be user friendly to those just looking to make mods.

If you do use, please read the documentation carefully and you should end up with viable NJA files (viable OBJ is included for demo purpose). Please let me know if you run into problems with the tool.

Happy modding~!

 

[egg yolk]

Today I am using njaPatcher to create test NJ files that I can analyze in a hex editor.

Since njaPatcher gives the freedom of creating models that can run through njaconv.exe, the specification for creating an NJ file should be the same as NJA specification except compressed and printed as binary. In theory, if an NJ file can be mapped out in correspondence to an NJA, it should be possible to use njaPatcher to directly print NJ files with a modified version of it's current algorithm, if a blank NJM was appended onto the end of the NJ file, this would remove two steps from the 3D modding pipeline in PSOBB. The final step would be writing an L7ZZ compression algorithm (PRSU) in JS.

Here are my findings with NJ so far using a cube model (no normals or textures, NJCM) as an example:

At 00000040 there are the values for different color/shading options. Not sure what the last byte is.

Next at 00000050 is the triangle strips, the first byte is saying "3 strips, first strip is size 10" and then it goes on to write the first triangle strip until 00000068. The byte starting on this line then says, "next strip is size 4" and continues etc.

The next section at 00000090 is verts, which seems to be the same order as the verts from NJA, except I'm unsure how it is converted, it seems like when a vert vector value is 0xc1a00000 then the hex value is that reversed, "00 00 A0 C1".

​

With this in mind, I will start to refactor njaPatcher today, the focus of the tool for now will be to allow arbitrary data injections into the patched NJA file, so that more precise testing can be done with NJ files.

 

[egg yolk]

Today I have been mostly figuring out how to generate NJTL and NJCM as binary (NJ file), I did make a huge amount of progress, but I can't say it works for sure, as I haven't tested enough to say so.

I did get massively sidetracked today since when testing njaPatcher NJA's through njaconv.exe, I found that a lot of the models were crashing when loaded in PSOBB. The crash usually occurs when doing a combo with another weapon and switching to the modded weapon in the process, e.g., when buffering weapon swap, or when switching between 2 modded weapons. Fortunately, I think I have found a solution to this, and will update the documentation for njaPatcher tomorrow if I confirm it.

With the testing that I have done tonight, I can say that the following is likely the solution to crashing models:

There is an extra requirement for loading textures, the texture in slot 0 always has to be the same dimensions as the texture originally in slot 0. For example, below is Diska of Braveman's texture file, since the original DoB "Texture 0" is 256x256, a 256x256 texture can replace it, but if the original texture was 128x128, the new texture would also have to be 128x128. I will try to confirm if this is the same for "Texture 1", but when looking at my previous mods, "Texture 1" seems to be flexible in terms of dimension (max 256x256).

EDIT: Read below post for confirmation on this, but it appears I was debugging the wrong object in general.

​

 

[egg yolk]

Okay, I can confirm that the above idea was not the solution to the crashing issue described. Instead the problem came from the NJM file I was appending onto the end of NJ files. To resolve this, the NJM from my previously released Dark Flow mod was used, which actually fixes the crashing issues. IIRC I had taken that NJM from a different weapon in PSOBB, but can't remember for sure.

With that said, I believe it's safe to use any squared texture size (max 256x256) in "Texture 0" as using the new NJM seems to fix the crashing.

There is another crash but it only occurs when exiting the game (alt bs twice), the crash occurs exactly before the game closes, perhaps some file check or something, not sure.

The above is partially irrelevant, since the in development version of njaPatcher now prints directly to binary NJ files as hex and appends an appropriate NJM anyway. This is the same as printing NJA, in that clicking on the hex within the browser will highlight the entire string. The below image shows it as a console log and in browser. There is no text wrapping implemented yet, but it doesn't stop the user from selecting the whole NJ string (see below).

​

I am not releasing this version of njaPatcher just yet, since I want to test that the new model conversions are stable, but it is looking good so far. It's also a bit of a mess in terms of codebase at the moment, so I will fix some things before I put a new version up. With this version of njaPatcher though, the 3D modding pipeline for ItemModelEp4 is now reduced to:

Make OBJ > OBJ 2 NJ (njaPatcher) > Save NJ file in a hex editor > Compress (PRS Utility) > Load into PSOBB (AFS Manager)

​

 

[egg yolk]

Today I am not working on any code, but have been testing model swaps. Below is a compatibility list for item swapping in terms of weapon category:

​

This of course will vary as some special weapons have unique properties. I've noticed with some weapons like Orotiagito, the special still works but has no visible projectile, so I am kind of interested in analyzing some weapon binaries to see if their visual effects can be extracted, and I also think that could be why the files in PSOBB are called XJ, since they have extra functionality, not sure if XJ is present in other SEGA games.

 

[egg yolk]

njaPatcher version 0.20a is now available to download from the repo - https://github.com/je-mappelle-egg-yolk/njaPatcher

This version of njaPatcher adds support for creating NJ files. If you wish to add them to PSOBB, please read the documentation carefully and refer to this post that I made a couple of days ago about the PSOBB modding pipeline: https://www.pioneer2.net/community/...conversion-from-obj-theory.20755/#post-171112.

With this release, njaPatcher can now output complete binary NJ files. Flashing NJA to NJ doesn't yet support objects without normals or texture coordinates, so it's not recommended if you want a shape like that, instead, if this type of model is required, flashNJ() should be disabled.

It's recommended to mess around with the program from within the "main.js" script, and to see what the program outputs when messing with the new functions, the default setup for this release will convert a weapon model (designed as a size reference) into a textured NJ file, that can be used in PSOBB after being saved in a hex editor and compressed with PRS utility.

Please let me know if you run into any bugs or problems.

^^b

 

[egg yolk]

Should be making another update to njaPatcher sometime this week/weekend. The update will get rid of a bug that causes an error when the OBJ has smoothing groups. If anyone had tried njaPatcher V0.20a and couldn't get it working, this is probably the reason.

Something else I have realized through researching XJ files is that, njaPatcher uses a very early alpha specification of NJA/NJ to generate models, the model structures it creates are pretty outdated compared to model files actually used in PSOBB, so there are many missing features between the two types, and there will be even when njaPatcher has complete NJA/NJ specification.

An example of a missing feature:

If you look at the mag Tellusis, it has a shadeless property on it's material, meaning it's geometry is always the exact colour of it's texture, njaPatcher does not have an option for this feature, and neither does the SEGA NJA/NJ exporter AFAIK, so a custom NJ model would need to be developed to get such a feature.

 

[egg yolk]

Some pretty big information just hit me after chatting with Shiva from Destiny PSOBB. If you export a model from 3DS MAX with grouped OBJs (separate files, same 3D editor scene) it draws bones between each object. This drastically changes how NJA and NJ is exported, since for each bone, NJA adds a new CHKOBJECT section with unique settings for position, angle, child, sibling, etc. This representation of NJ is actually very different to exporting from a single OBJ, which is what I have been doing, and it looks closer to XJ.

It makes sense to look like XJ, since small files like the lock on cursor are similar to single OBJ export of NJ, since they are a single 3D model.

I will look at NJ binary from the start again, the first test will see how a cube split in two will look, this will hopefully create 2 bones (one for each half). I will gradually increase the bone count by splitting the cube further, but won't increase the amount of verts that it has, some part of the file should stay static if I can carry out this test, but I am leaving it for the moment.